|
libTheSky
Routines to compute sky positions of Sun, Moon, planets and more
|
 |
libTheSky
Routines to compute sky positions of Sun, Moon, planets and more
|
Procedures for planets. More...
Functions/Subroutines | |
| subroutine | planet_position (jd, pl, lat, lon, hgt, lbaccur, raccur, ltime, aber, to_fk5, assume_jde, lunar_theory, nutat, magmdl, verbosity) |
| Compute the position, distance, etc of a planet. | |
| subroutine | plutolbr (t, l, b, r) |
| Calculate Pluto's position l,b,r at time t. | |
| subroutine | planetelements (jd) |
| Calculate orbital elements for the planets. | |
| real(double) function | planet_magnitude (pl, hc_dist, gc_dist, phang, model) |
| Calculate planet magnitude. | |
| real(double) function | satmagn (t, gl, gb, d, l, b, r, magmdl) |
| Calculate Saturn's magnitude. | |
| real(double) function | dsatmagn (tjc, glon, glat) |
| Calculate a correction to Saturn's magnitude due to its rings. | |
| subroutine | earthshadow (dm0, ds0, r1, r2) |
| Calculate the umbra and penumbra geocentric radii of the Earth's shadow. | |
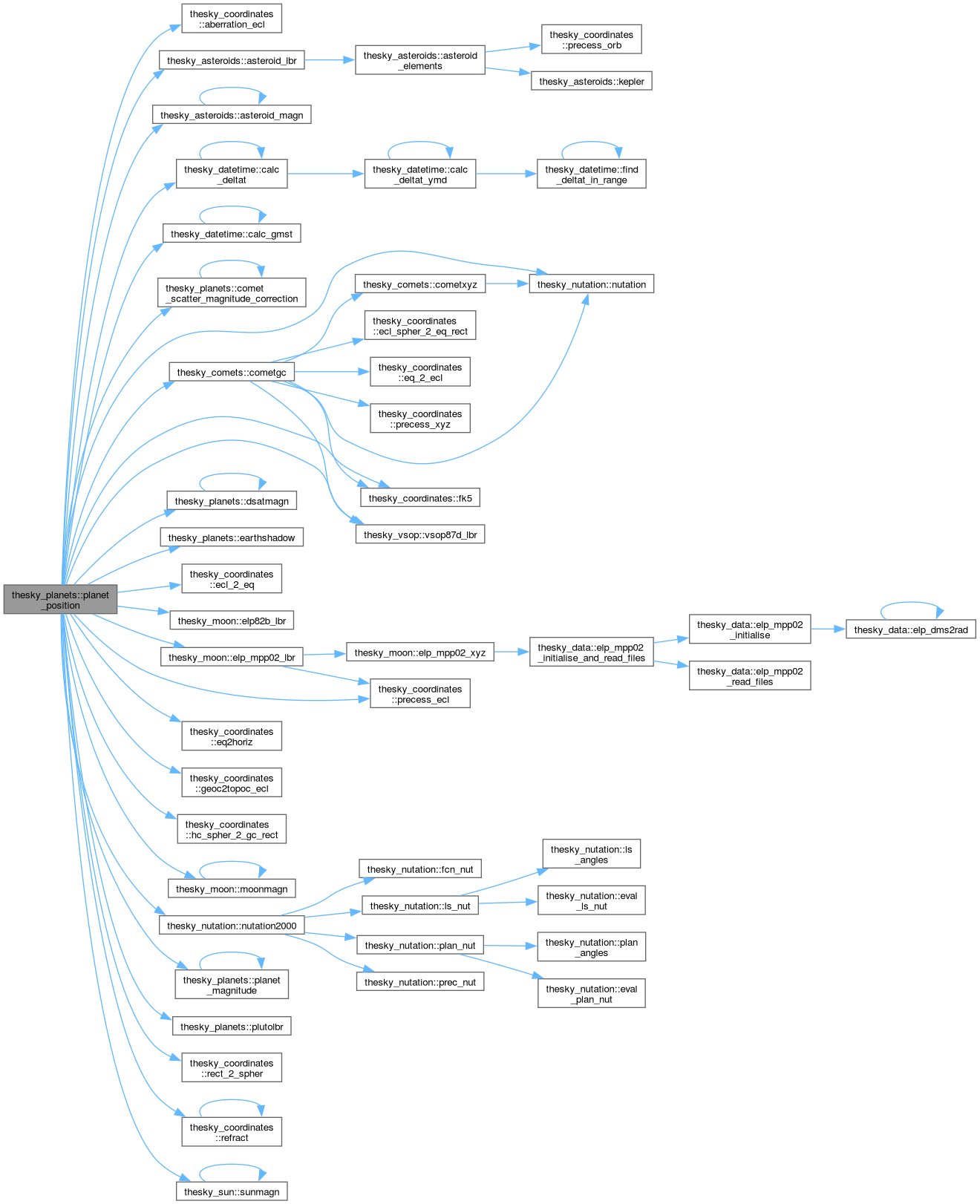
| subroutine | jupiterphys (jd, de, ds, omg1, omg2, dphase, pa, in, om) |
| Compute physical data for Jupiter. | |
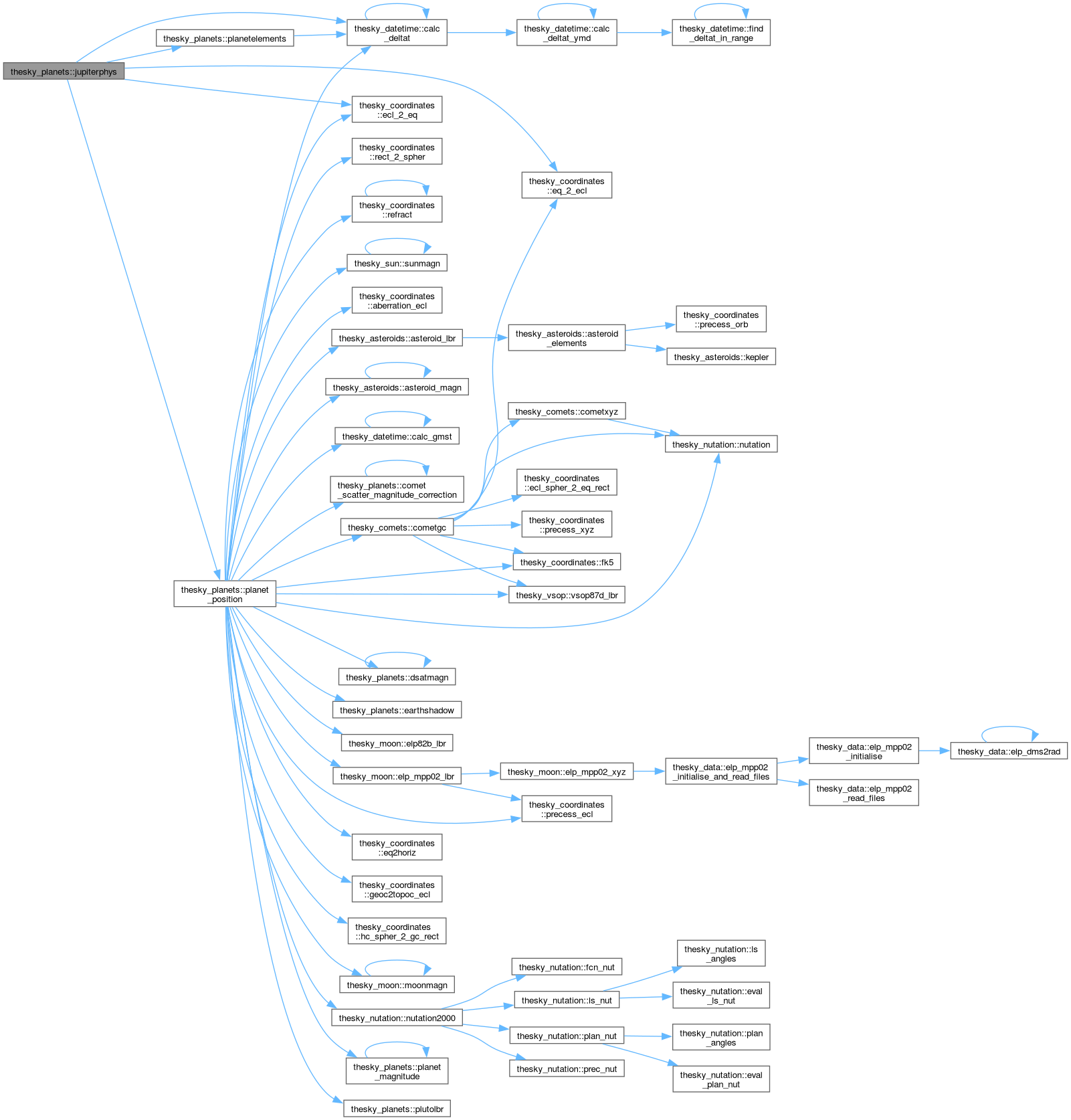
| subroutine | saturnphys (jd, be, bs, pa, in, om, ar, br, du, pa_s, ar_s, br_s) |
| Compute physical data for Saturn. | |
| subroutine | planet_position_la (jd, pl, calc, nt, lat, lon) |
| Compute low-accuracy planet positions. Sun and Moon have dedicated routines, for planets abridged VSOP87 is used. | |
| real(double) function | comet_scatter_magnitude_correction (phaseang) |
| Correction for comet magnitude due to forward and backscattering. | |
Procedures for planets.
| real(double) function thesky_planets::comet_scatter_magnitude_correction | ( | real(double), intent(in) | phaseang | ) |
Correction for comet magnitude due to forward and backscattering.
| phaseAng | Phase angle of the comet (rad) |
| Magnitude | correction, to be added to the magnitude (usually negative) |
Definition at line 1319 of file planets.f90.
References comet_scatter_magnitude_correction().
Referenced by comet_scatter_magnitude_correction(), and planet_position().

| real(double) function thesky_planets::dsatmagn | ( | real(double), intent(in) | tjc, |
| real(double), intent(in) | glon, | ||
| real(double), intent(in) | glat ) |
Calculate a correction to Saturn's magnitude due to its rings.
| tjc | Dynamical time in Julian centuries after J2000.0. |
| glon | Geocentric longitude (rad). |
| glat | Geocentric latitude (rad). |
| dsatmagn | Correction to Saturn's magnitude due to its rings. |
Definition at line 907 of file planets.f90.
References dsatmagn().
Referenced by dsatmagn(), and planet_position().

| subroutine thesky_planets::earthshadow | ( | real(double), intent(in) | dm0, |
| real(double), intent(in) | ds0, | ||
| real(double), intent(out) | r1, | ||
| real(double), intent(out) | r2 ) |
Calculate the umbra and penumbra geocentric radii of the Earth's shadow.
| dm0 | Distance of the Moon (AU) |
| ds0 | Distance of the Sun (AU) |
| r1 | Umbra radius at distance of the Moon (rad) (output) |
| r2 | Penumbra radius at distance of the Moon (rad) (output) |
Definition at line 937 of file planets.f90.
Referenced by planet_position().
| subroutine thesky_planets::jupiterphys | ( | real(double), intent(in) | jd, |
| real(double), intent(out) | de, | ||
| real(double), intent(out) | ds, | ||
| real(double), intent(out) | omg1, | ||
| real(double), intent(out) | omg2, | ||
| real(double), intent(out) | dphase, | ||
| real(double), intent(out) | pa, | ||
| real(double), intent(out) | in, | ||
| real(double), intent(out) | om ) |
Compute physical data for Jupiter.
| jd | Julian day for computation |
| de | Jovocentric latitude of the Earth = inclination of planet axis to plane of the sky as seen from Earth (output) |
| ds | Jovocentric latitude of the Sun = inclination of planet axis to plane of the sky as seen from Earth (output) |
| omg1 | Longitude of central meridian of System I (equator+-10deg) (output) |
| omg2 | Longitude of central meridian of System II (output) |
| dphase | Phase correction (output) |
| pa | Position angle of Jupiter's north pole (from N to E) (output) |
| in | Inclination of Jupiter's rotation axis to the orbital plane (output) |
| om | Longitude of node of Jupiter's equator on ecliptic (output) |
Definition at line 980 of file planets.f90.
References thesky_datetime::calc_deltat(), thesky_local::deltat, thesky_coordinates::ecl_2_eq(), thesky_coordinates::eq_2_ecl(), planet_position(), planetelements(), and thesky_planetdata::planpos.
| real(double) function thesky_planets::planet_magnitude | ( | integer, intent(in) | pl, |
| real(double), intent(in) | hc_dist, | ||
| real(double), intent(in) | gc_dist, | ||
| real(double), intent(in) | phang, | ||
| integer, intent(in), optional | model ) |
Calculate planet magnitude.
| pl | Planet ID |
| hc_dist | Distance from the Sun (AU) |
| gc_dist | Distance from the Earth (AU) |
| phang | Phase angle (rad) |
| model | Model to use: 1: Müller (1893), 2: Meeus p.286, 3: AA 1992, 4: AA 2012 (optional, defaults to 4). |
| planet_magnitude | Apparent visual planet magnitiude |
Definition at line 771 of file planets.f90.
References planet_magnitude().
Referenced by planet_magnitude(), and planet_position().

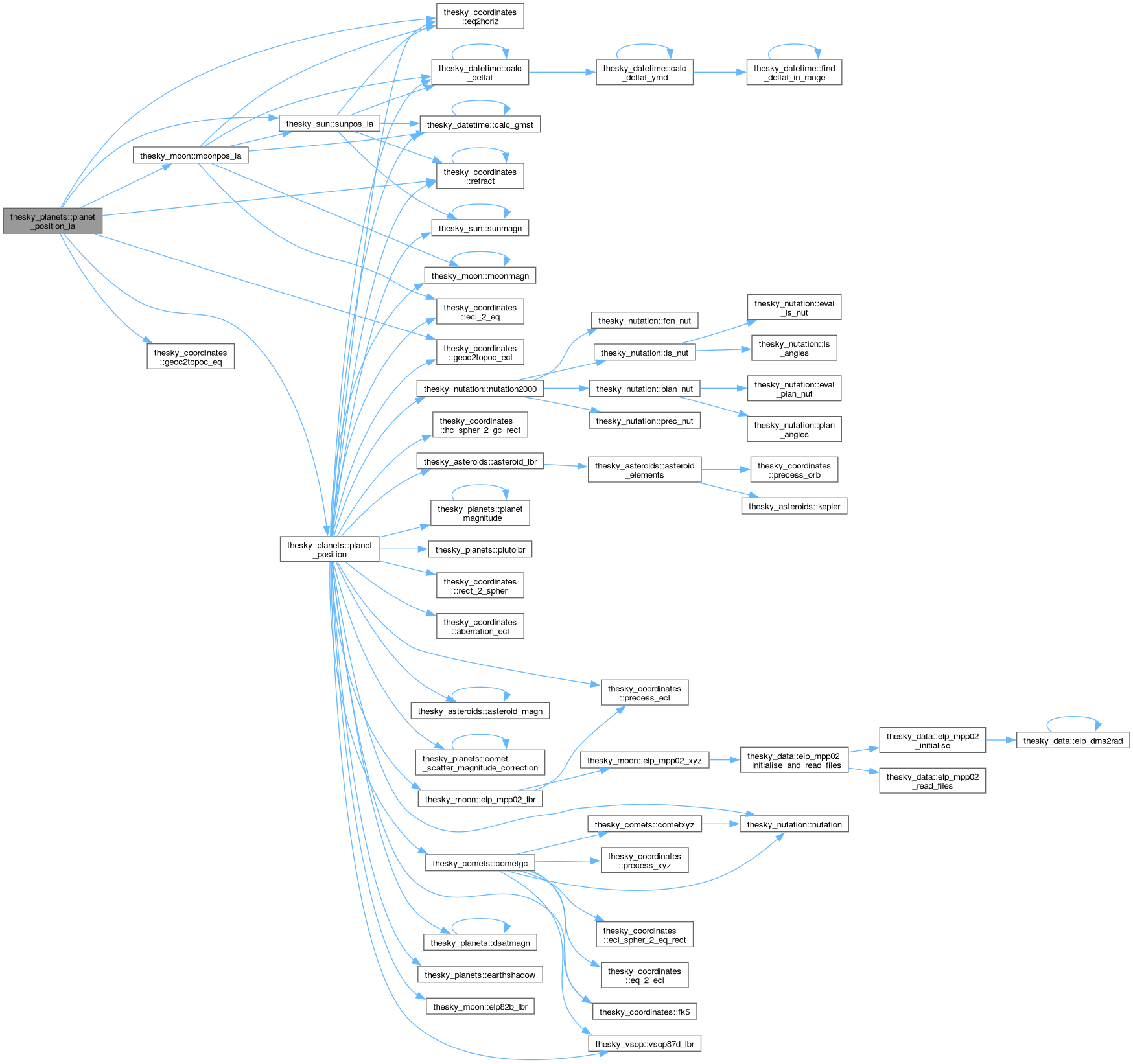
| subroutine thesky_planets::planet_position | ( | real(double), intent(in) | jd, |
| integer, intent(in) | pl, | ||
| real(double), intent(in), optional | lat, | ||
| real(double), intent(in), optional | lon, | ||
| real(double), intent(in), optional | hgt, | ||
| real(double), intent(in), optional | lbaccur, | ||
| real(double), intent(in), optional | raccur, | ||
| logical, intent(in), optional | ltime, | ||
| logical, intent(in), optional | aber, | ||
| logical, intent(in), optional | to_fk5, | ||
| logical, intent(in), optional | assume_jde, | ||
| integer, intent(in), optional | lunar_theory, | ||
| integer, intent(in), optional | nutat, | ||
| integer, intent(in), optional | magmdl, | ||
| integer, intent(in), optional | verbosity ) |
Compute the position, distance, etc of a planet.
| jd | Julian date of computation |
| pl | Planet number: Moon=0, Merc=1,Nep=8,Plu=9 3=Sun, 0=Moon, >10 for other objects |
| lat | Latitude of the observer (rad, optional) |
| lon | Longitude of the observer (rad, optional) |
| hgt | Altitude/elevation of the observer above sea level (metres, optional) |
| LBaccur | Desired accuracy of the heliocentric L,B in VSOP87 (rad, optional; defaults to full accuracy) |
| Raccur | Desired accuracy of the heliocentric R in VSOP87 (AU, optional; defaults to full accuracy) |
| ltime | Correct for light time (optional; defaults to true). .false. saves ~50% in CPU time at the cost of some accuracy. |
| aber | Correct for aberration (optional; defaults to true). |
| to_fk5 | Convert coordinates to the FK5 system (optional; defaults to true). |
| assume_jde | Assume JD provided is actually JDE (optional; defaults to false). |
| lunar_theory | Choose Lunar theory: 1: ELP82b, 2: ELP-MPP02/LLR, 3: ELP-MPP02/DE405 ('historical' - default) |
| nutat | IAU nutation model to use: 0 (no nutation!), 1980 or 2000 (default). |
| magmdl | Planet-magnitude model: 1: Müller (1893), 2: Meeus p.286, 3: AA 1992, 4: AA 2012 (optional, defaults to 4). |
| verbosity | Verbosity for debug output (0-3). Defaults to 0: silent. |
Definition at line 61 of file planets.f90.
References thesky_coordinates::aberration_ecl(), thesky_asteroids::asteroid_lbr(), thesky_asteroids::asteroid_magn(), thesky_datetime::calc_deltat(), thesky_datetime::calc_gmst(), comet_scatter_magnitude_correction(), thesky_cometdata::cometdiedatp, thesky_cometdata::cometelems, thesky_comets::cometgc(), thesky_local::deltat, dsatmagn(), earthshadow(), thesky_coordinates::ecl_2_eq(), thesky_moon::elp82b_lbr(), thesky_moon::elp_mpp02_lbr(), thesky_coordinates::eq2horiz(), thesky_coordinates::fk5(), thesky_coordinates::geoc2topoc_ecl(), thesky_coordinates::hc_spher_2_gc_rect(), thesky_local::height, thesky_local::lat0, thesky_local::lon0, thesky_moon::moonmagn(), thesky_nutation::nutation(), thesky_nutation::nutation2000(), thesky_planetdata::pl0, planet_magnitude(), thesky_planetdata::planpos, plutolbr(), thesky_coordinates::precess_ecl(), thesky_coordinates::rect_2_spher(), thesky_coordinates::refract(), thesky_sun::sunmagn(), and thesky_vsop::vsop87d_lbr().
Referenced by thesky_riset::best_obs_date(), thesky_visibility::best_planet_visibility(), thesky_visibility::get_dra_obj(), jupiterphys(), thesky_moonroutines::moonphys(), planet_position_la(), thesky_functions::plpa(), thesky_functions::plsep(), thesky_riset::riset(), thesky_riset::riset_ad(), thesky_riset::riset_ipol(), and saturnphys().
| subroutine thesky_planets::planet_position_la | ( | real(double), intent(in) | jd, |
| integer, intent(in) | pl, | ||
| integer, intent(in), optional | calc, | ||
| integer, intent(in), optional | nt, | ||
| real(double), intent(in), optional | lat, | ||
| real(double), intent(in), optional | lon ) |
Compute low-accuracy planet positions. Sun and Moon have dedicated routines, for planets abridged VSOP87 is used.
| jd | Julian Day of computation |
| pl | Planet number: 0: Moon, 1-2: Mer-Ven, 3: Sun, 4-9: Mar-Plu |
| calc | Calculate 1: l,b,r,diam, 2: + ra,dec, 3: + gmst,agst, 4: + az,alt, 5: + elon, mag, k, pa, parang, hp, GC LBR, 6: + topocentric positions (Sun and Moon only, optional - default = 5) |
| nt | Number of terms to use for the calculation (has an effect for Moon only; nt<=60); a smaller nt gives faster, but less accurate results (optional, default=60) |
| lat | Latitude of the observer (rad, optional) |
| lon | Longitude of the observer (rad, optional) |
Definition at line 1226 of file planets.f90.
References thesky_coordinates::eq2horiz(), thesky_coordinates::geoc2topoc_ecl(), thesky_coordinates::geoc2topoc_eq(), thesky_local::lat0, thesky_local::lon0, thesky_moon::moonpos_la(), planet_position(), thesky_planetdata::planpos, thesky_coordinates::refract(), and thesky_sun::sunpos_la().
Referenced by thesky_visibility::limmag_jd(), thesky_visibility::limmag_jd_pl(), thesky_visibility::pl_xsmag(), thesky_visibility::pl_xsmag_la(), and thesky_riset::riset().
| subroutine thesky_planets::planetelements | ( | real(double), intent(in) | jd | ) |
Calculate orbital elements for the planets.
| jd | Julian day of calculation |
Definition at line 700 of file planets.f90.
References thesky_datetime::calc_deltat(), thesky_local::deltat, thesky_planetdata::plelemdata, thesky_planetdata::plelems, and thesky_planetdata::plelems2000.
Referenced by jupiterphys(), and saturnphys().

| subroutine thesky_planets::plutolbr | ( | real(double), intent(in) | t, |
| real(double), intent(out) | l, | ||
| real(double), intent(out) | b, | ||
| real(double), intent(out) | r ) |
Calculate Pluto's position l,b,r at time t.
| t | Dynamical time in Julian Centuries after 2000.0 |
| l | Heliocentric longitude (rad) (output) |
| b | Heliocentric latitude (rad) (output) |
| r | Heliocentric distance (AU?) (output) |
Definition at line 643 of file planets.f90.
References thesky_planetdata::plub, thesky_planetdata::pluc, thesky_planetdata::plul, and thesky_planetdata::plur.
Referenced by planet_position().
| real(double) function thesky_planets::satmagn | ( | real(double), intent(in) | t, |
| real(double), intent(in) | gl, | ||
| real(double), intent(in) | gb, | ||
| real(double), intent(in) | d, | ||
| real(double), intent(in) | l, | ||
| real(double), intent(in) | b, | ||
| real(double), intent(in) | r, | ||
| integer, intent(in), optional | magmdl ) |
Calculate Saturn's magnitude.
| t | Dynamical time in Julian centuries after J2000.0 |
| gl | Geocentric longitude (rad) |
| gb | Geocentric latitude (rad) |
| d | Geocentric distance (AU) |
| l | Heliocentric longitude (rad) |
| b | Heliocentric latitude (rad) |
| r | Heliocentric distance (AU) |
| magmdl | Model to use: 1: Müller (1893), 2: Meeus p.286; optional, default: 2. |
| satmagn | The magnitude of Saturn |
Definition at line 857 of file planets.f90.
References satmagn().
Referenced by satmagn().

| subroutine thesky_planets::saturnphys | ( | real(double), intent(in) | jd, |
| real(double), intent(out) | be, | ||
| real(double), intent(out) | bs, | ||
| real(double), intent(out) | pa, | ||
| real(double), intent(out) | in, | ||
| real(double), intent(out) | om, | ||
| real(double), intent(out) | ar, | ||
| real(double), intent(out) | br, | ||
| real(double), intent(out) | du, | ||
| real(double), intent(out) | pa_s, | ||
| real(double), intent(out) | ar_s, | ||
| real(double), intent(out) | br_s ) |
Compute physical data for Saturn.
| jd | Julian day of computation |
| be | Saturnicentric latitude of the Earth = inclination of planet axis to plane of the sky as seen from Earth (output) |
| bs | Saturnicentric latitude of the Sun = inclination of planet axis to plane of the sky as seen from the Sun (output) |
| pa | Position angle of Saturn's north pole (from N to E) (output) |
| in | Inclination of Saturn's rotation axis to the orbital plane (output) |
| om | Longitude of node of Saturn's equator on ecliptic (output) |
| ar | Projected major axis of ring (NOT semi-!!!) (output) |
| br | Projected minor axes of ring (NOT semi-!!!), = ar * sin(be) (output) |
| du | Difference between saturnicentric longitudes of Sun and Earth (Sun - Earth, NOT abs!!!) (output) |
| pa_s | Position angle of Saturn's north pole (from N to E), as seen from the SUN (output) |
| ar_s | Projected major axis of ring (NOT semi-!!!), as seen from the SUN (output) |
| br_s | Projected minor axes of ring (NOT semi-!!!), as seen from the SUN, = ar_s * sin(bs) (output) |
Definition at line 1104 of file planets.f90.
References thesky_coordinates::ecl_2_eq(), thesky_coordinates::hc_spher_2_gc_rect(), planet_position(), planetelements(), thesky_planetdata::planpos, thesky_planetdata::plelems, and thesky_coordinates::rect_2_spher().